Table des matières
Quelques figues géométriques...
Nous allons commencer très simple : tracer quelques figures géométriques de base : le carré et le rectangle…
Inducteur : tracer un carré, tracer un rectangle
Maintenant qu'ils savent se déplacer, on peut facilement leur demander de dessiner un carré ou un rectangle.
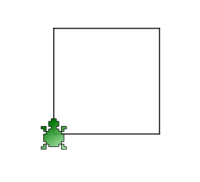
Le carré
Préalable, si nécessaire, réaliser la construction en géométrie et faire réaliser le protocole de traçage: Pour le carré
- Tracer un segment de 5 cm - "Tourner" de 90° (angle droit) - Tracer un segment de 5 cm - "Tourner" de 90° (angle droit) - Tracer un segment de 5 cm - "Tourner" de 90° (angle droit) - Tracer un segment de 5 cm - "Tourner" de 90° (angle droit)
reset forward 100 turnright 90 forward 100 turnright 90 forward 100 turnright 90 forward 100 turnright 90
En géométrie, on utiliser comme unité celles des longueurs : cm, mm, etc…
En programmation sur PC, on utilisera l'unité de l'écran (notion de résolution (pixel par surface définie)) c'est à dire le pixel
Donc forward 50, c'est tracer une ligne de 50 pixels.
Mes élèves n'ont pas eu de soucis avec cela car l'année précédente, ils ont travaillé sur “1,2,3 codez” (https://cbiot.fr/dokuwiki/doku.php?id=aseba:seances-4-5 | cf cette séance)
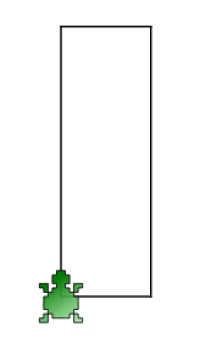
Le rectangle
- Tracer un segment de 5 cm - "Tourner" de 90° (angle droit) - Tracer un segment de 2 cm - "Tourner" de 90° (angle droit) - Tracer un segment de 5 cm - "Tourner" de 90° (angle droit) - Tracer un segment de 5 cm - "Tourner" de 90° (angle droit)
reset forward 150 turnright 90 forward 50 turnright 90 forward 150 turnright 90 forward 50 turnright 90
Si les valeurs sont trop importantes, la figure dépassera de la zone de dessin. Demander de modifier les valeurs par des valeurs plus petites. Nous aborderons cette remédiation dans une autre séance.
Le triangle
Très vite les enfants voudront d'eux même réaliser d'autres figures dont les triangles. Leur codage est simple pour les triangles équilatéraux : 3 cotés de la même longueur et 3 angles égaux (qu'ils peuvent trouver car en cycle 3, ils savent que la somme des angles du triangle est égale à 180 degrés, donc la valeur de l'angle est de 60).
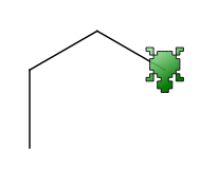
Ils proposeront alors comme code
reset forward 50 turnright 60 forward 50 turnright 60 forward 50 turnright 60
En effet, il faut en fait tourner de 180 ° - 60 ° soit de 120 ° . Pour leur expliquer le mieux est de découper des gabarit d'angles et de leur faire miner les déplacements.
Notez que les élèves diront c'est un hexagone ! Mais incomplet ! Leur demander combien, il manque de cotés et leur faire compléter leur code… Façon assez simple de dessiner un hexagone suite à une erreur …
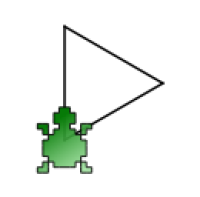
Le code devient alors
reset forward 50 turnright 120 forward 50 turnright 120 forward 50 turnright 120
L'hexagone
Suite à l'erreur précédente lors du codage du triangle, on demande aux élèves de compléter leur code afin d'obtenir un hexagone, cette fois-ci complet. Comme le code précédent n'a donné qu'un demi hexagone, il suffit de le copier une nouvelle fois ;). Ce qui donne :
reset forward 50 turnright 60 forward 50 turnright 60 forward 50 turnright 60 forward 50 turnright 60 forward 50 turnright 60 forward 50 turnright 60
Navigation
| page précédente | Sommaire | Page suivante |
|---|---|---|
| A la découverte de Kturtle | sommaire | Quelques figures géométriques (suite) |