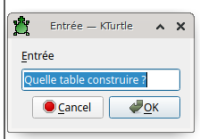
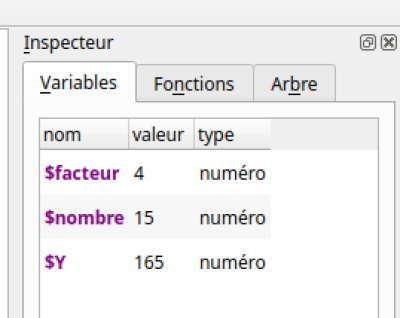
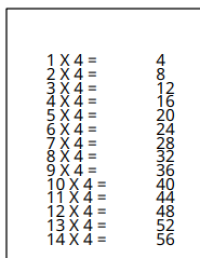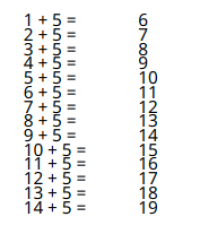FOLLOW ...
Linux, freeBSD
Python
Plugins WP
Informatique et robotique
En classe
- Programmation et robotique en classe. Algorithmes et Scratch.
- Programmation et robotique en classe. Encoder une image.
- Robotique : Thymio, séance découverte. Découverte de Thymio et de VPL.